Random ODE

Key word

• Hermite展開，Galerkin法
• 放射能半減，調和振動子

はじめに

常微分方程式（ODE）の初期条件や係数が不確実な場合にはそれを方程式に盛り込む必要があります． ここでは初期条件や定数係数が確率変数であるODEをRandom ODE¹と呼び，それについて考えます． Hermite展開とGalerkin近似によるRandom ODEの数値解法を紹介します²． Hermite展開に基づいています．

放射能半減

方程式

$ \lambda, b > 0 $ に対して以下のような単純な放射能半減の微分方程式を考える．

$ \dot{u}(t) = - \lambda u(t), \hspace{1em} u(0) = b $

$ \lambda, b $ が不確実な場合を考え，上記の方程式をRandom ODEとして捉えます．

ここでは $ \lambda, b $ がGaussianに従うとして，以下が実現される．

• Hermite展開により確率変数の「成分表示」．
• Galerkin productにより確率変数の「成分表示による積」を定義．

解

展開を有限項で打ち切ることにより数値的に解けます． 数値解のHermite展開係数から解のモーメントを計算することができます．

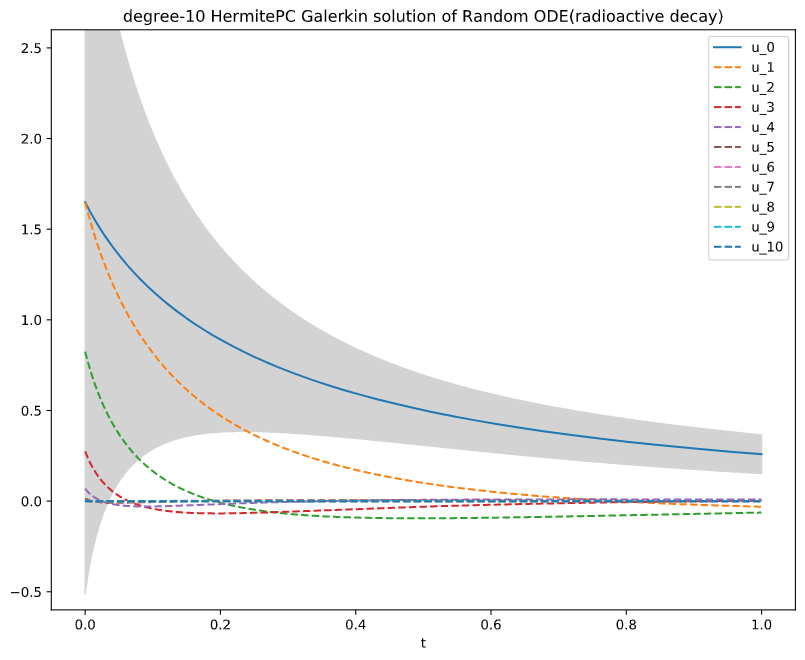
調和振動子

結果画像

pdf

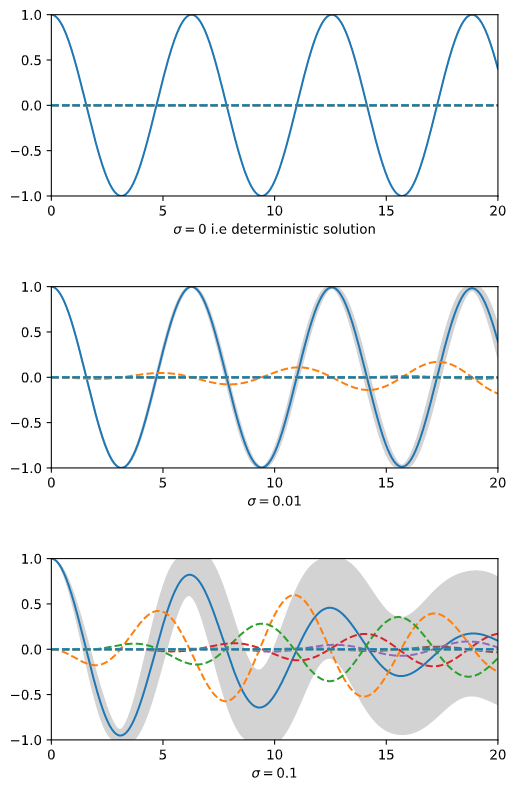
もう一つの例(調和振動子)と詳細な説明は以下のpdfにあります．

詳細はこちら

まとめ

• Random ODEの数値解法と計算結果を示しました．
• Hermite展開により乱数を発生させずにRandomな現象を扱うことができます．
• Galerkin productにより確率変数の積にも対応できます．

参考

• Timothy John Sullivan. Introduction to uncertainty quantification, Springer, 2015.

注意

1. 用語として確率微分方程式(Stochastic Differential Equation: SDE)とは区別されるべきです． ↩

2. 確率微分方程式を解くわけではないので確率積分は行わず，したがってdeterministicに解けます． ↩