Probabilistic ODE Solver

Key word

• ODE
• Probabilistic Numerics

概要

Winner過程の積分を用いて確率的にODEを解く方法についてのメモ．

ODEの初期値問題

$ y’(t) = f(t, y), \quad y(0) = y_0 $

を解くために，Winner過程を走らせて，ODEに合わせる作業する．

状態変数として，$ y’$に対応するWinner過程 $ W^1 $とその積分 $ W^0 $($ y $に対応)を考える．

$ W^0 = W^1 dt, \quad W^1_t = dB_t $

観測 $ H: \begin{bmatrix} W^0
W^1 \end{bmatrix} \rightarrow \begin{bmatrix} 0
f(t, y) \end{bmatrix} $ により状態を補正．

補正にはKalman Filterを用いる．

メリット

• implicitにODEを解ける．

実装

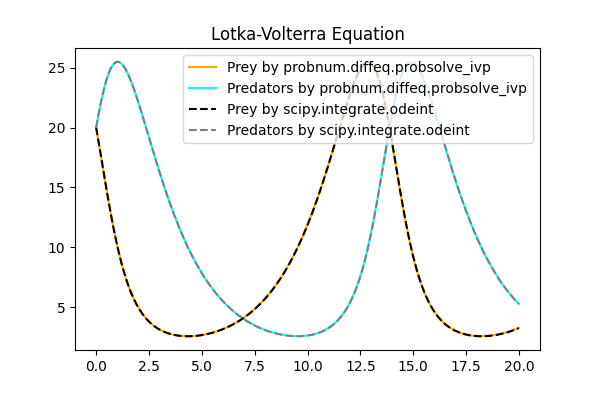
probnumとしてPythonによる実装がある．

Lotka-Volterra方程式に対して，scipy.integrate.odeintと比較した．

参考

• ODE Solver Research
• probabilistic-numerics.org
• ProbNum Docs
• https://arxiv.org/pdf/2012.08202.pdf
• https://arxiv.org/pdf/1610.05261.pdf