線形半群の初期挙動とNumerical Abscissa

問題

以下の2つの行列 $A=A_1, A_2$について, 半群のノルム$|e^{tA}|$($t \ge 0$)の時間発展を考える.

\[A_1 = \left( \begin{array}{cc} -1 & 1 \\ 0 & -1 \end{array} \right), \quad A_2 = \left( \begin{array}{cc} -1 & 5 \\ 0 & -2 \end{array} \right).\]

それぞれ, 固有値は全て負なので$t \rightarrow \infty$ではノルムは減衰する. しかし, $t=0$付近での挙動(Transient behaviourとも呼ぶ)は，行列$A$の非対称(非正規)性により固有値だけでは決まらず, 一時的にノルムが大きくなることがある.

Transient behaviourの特徴づけの一つとして, $t=0$でのノルム変化率を調べる.

\[\frac{d}{dt} \|e^{tA}\| |_{t=0}.\]

参考文献[1]によると, これはNumerical abscissa $\omega(A)$と呼ばれる行列$A$から定まる量で

\[\frac{d}{dt} \|e^{tA}\| |_{t=0} = \omega(A).\]

と計算できる. 今の設定では, Numerical abscissaは

\[\omega(A) = \sup \sigma \left(\frac{1}{2}(A + A^\top)\right)\]

となる. ただし, $\sigma(A)$は行列のスペクトルである.

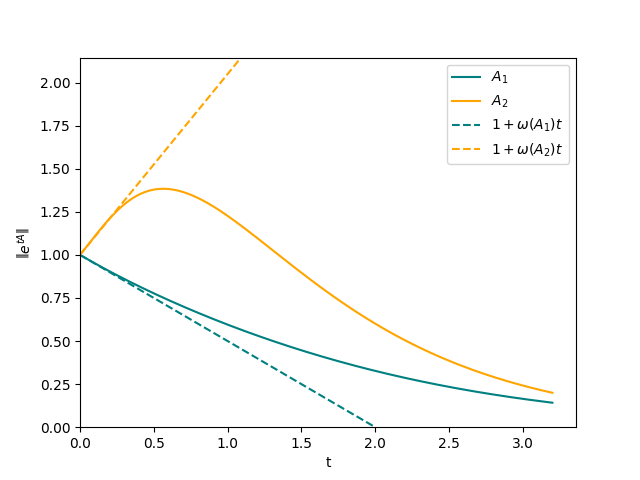
以下では, $A=A_1, A_2$について, 半群のノルム$|e^{tA}|$($t \ge 0$)の時間発展をプロットし, $t=0$での傾きとNumerical abscissa $\omega(A)$を比較する.

$numerical abscissa$

実装:

[1] Trefethen, L.N., Embree, M., 2005. Spectra and Pseudospectra: The Behavior of Nonnormal Matrices and Operators. Princeton University Press, Princeton.